Гравитационная энергия. Потенциальная энергия гравитационного взаимодействия

В связи с рядом особенностей, а также ввиду особой важности вопрос о потенциальной энергии сил всемирного тяготения необходимо рассмотреть отдельно и более детально.

С первой особенностью мы сталкиваемся при выборе начала отсчета потенциальных энергий. На практике приходится рассчитывать движения данного (пробного) тела под действием сил всемирного тяготения, создаваемых другими телами разных масс и размеров.

Допустим, что мы условились считать равной нулю потенциальную энергию при таком положении, при котором тела соприкасаются. Пусть пробное тело А при взаимодействии по отдельности с шарами одинаковой массы, но разных радиусов, вначале удалено от центров шаров на одно и то же расстояние (рис. 5.28). Нетрудно видеть, что при движении тела А до соприкосновения с поверхностями тел силы тяготения совершат разную работу. Это значит, что мы должны при одинаковых относительных начальных расположениях тел считать потенциальные энергии систем различными.

Сопоставлять эти энергии между собой будет особо затруднительно в случаях, когда рассматриваются взаимодействия и движения трех или большего количества тел. Поэтому для сил всемирного тяготения ищется такой начальный уровень отсчета потенциальных энергий, который бы мог быть одинаковым, общим, для всех тел во Вселенной. Таким общим нулевым уровнем потенциальной энергии сил всемирного тяготения условились считать уровень, соответствующий расположению тел на бесконечно больших расстояниях друг от друга. Как видно из закона всемирного тяготения, на бесконечности обращаются в нуль и сами силы всемирного тяготения.

При таком выборе начала отсчета энергий создается непривычное положение с определением значений потенциальных энергий и проведением всех расчетов.

В случаях сил тяжести (рис. 5.29, а) и упругости (рис. 5.29, б) внутренние силы системы стремятся привести тела на нулевой уровень. При приближении тел к нулевому уровню потенциальная энергия системы уменьшается. Нулевому уровню действительно соответствует наименьшая потенциальная энергия системы.

Это означает, что при всех других положениях тел потенциальная энергия системы положительна.

В случае сил всемирного тяготения и при выборе нуля энергии на бесконечности все происходит наоборот. Внутренние силы системы стремятся увести тела от нулевого уровня (рис. 5.30). Они совершают положительную работу при удалении тел от нулевого уровня, т. е. при сближении тел. При любых конечных расстояниях между телами потенциальная энергия системы меньше, чем при Другими словами, нулевому уровню (при соответствует наибольшая потенциальная энергия. Это означает, что при всех других положениях тел потенциальная энергия системы отрицательна.

В § 96 было найдено, что работа сил всемирного тяготения при переносе тела из бесконечности на расстояние равна

Поэтому потенциальную энергию сил всемирного тяготения нужно считать равной

Эта формула выражает еще одну особенность потенциальной энергии сил всемирного тяготения - сравнительно сложный характер зависимости этой энергии от расстояния между телами.

На рис. 5.31 представлен график зависимости от для случая притяжения тел Землей. Этот график имеет вид равнобочной гиперболы. Вблизи поверхности Земли энергия меняется сравнительно сильно, но уже на расстоянии нескольких десятков земных радиусов энергия становится близкой к нулю и начинает меняться очень медленно.

Любое тело вблизи поверхности Земли находится в своеобразной «потенциальной яме». Всякий раз, когда оказывается необходимым освободить тело от действия сил земного притяжения, нужно прилагать специальные усилия для того, чтобы «вытащить» тело из этой потенциальной ямы.

Точно так же и все другие небесные тела создают вокруг себя такие потенциальные ямы - ловушки, которые захватывают и удерживают все не очень быстро движущиеся тела.

Знание характера зависимости от позволяет значительно упростить решение ряда важных практических задач. Например, необходимо послать космический корабль на Марс, Венеру или на любую другую планету Солнечной системы. Нужно определить, какая скорость должна быть сообщена кораблю при его запуске с поверхности Земли.

Для того чтобы корабль послать к другим планетам, его нужно вывести из сферы действия сил земного притяжения. Другими словами, нужно поднять его потенциальную энергию до нуля. Это становится возможным, если кораблю сообщить такую кинетическую энергию, чтобы он смог совершить работу против сил земного притяжения, равную где масса корабля,

масса и радиус земного шара.

Из второго закона Ньютона следует, что (§ 92)

Но так как скорость корабля до запуска равна нулю, то можно записать просто:

где скорость, сообщаемая кораблю при запуске. Подставляя значение для А, получим

Воспользуемся для исключения как это уже делали в § 96, двумя выражениями для силы земного притяжения на поверхности Земли:

Отсюда - Подставляя это значение в уравнение второго закона Ньютона, получим

Скорость, необходимая для вывода тела из сферы действия сил земного притяжения, называется второй космической скоростью.

Точно так же можно поставить и решить задачу о посылке корабля к далеким звездам. Для решения такой задачи нужно уже определить условия, при которых корабль будет выведен из сферы действия сил притяжения Солнца. Повторяя все рассуждения, которые были проведены в предыдущей задаче, можно получить такое же выражение для скорости, сообщаемой кораблю при запуске:

Здесь а - нормальное ускорение, которое сообщает Солнце Земле и которое может быть рассчитано по характеру движения Земли по орбите вокруг Солнца; радиус земной орбиты. Конечно, в этом случае означает скорость движения корабля относительно Солнца. Скорость, необходимая для вывода корабля за пределы Солнечной системы, называется третьей космической скоростью.

Рассмотренный нами способ выбора начала отсчета потенциальной энергии используется и при расчетах электрических взаимодействий тел. Представление о потенциальных ямах также широко используется в современной электронике, теории твердого тела, теории атома и в физике атомного ядра.

Установленный Ньютоном закон всемирного тяготения гласит:

ОПРЕДЕЛЕНИЕ: Гравитационная сила илисила тяготения – это сила, с которой две материальные точки притягивают друг друга, пропорциональная массам этих точек и обратно пропорциональная квадрату расстояния между ними, где– гравитационная постоянная. Эта сила направлена вдоль прямой, проходящей через взаимодействующие материальные точки.

Рассмотрим два тела массами m 1 ,m 2 (считаем их материальными точками) и будем их сближать от расстоянияr 1 доr 2 .

Элементарная работа на пути dr будет
. Полная работа

Т.е.
. Величина

(3.11)

называется потенциальной энергией тела в поле всемирного тяготения.

Если между телами действует сила притяжения, то U p <0;

если между телами действует сила отталкивания, то U p >0.

Из выражения (3.11) следует, что максимальное значение потенциальной энергии тяготеющие тела будут иметь тогда, когда они бесконечно (r=) удалены друг от друга (U p = 0).

Введем величину называемую потенциалом гравитационного поля.

ОПРЕДЕЛЕНИЕ: Потенциал – это скалярная величина, численно равная работе по перемещению в гравитационном поле тела единичной массы из данной точки поля на бесконечность (r=).

;
или
. Поле можно характеризовать потенциальной энергией, которой обладает в данном месте материальная точка.

Получаем, что
. Зная потенциал, можно вычислить работу, совершаемую над частицей массой «m» силами поля при перемещении ее из положения 1 в положение 2:.

В потенциальном поле можно провести поверхность, имеющую одинаковый потенциал. Такая поверхность называется эквипотенциальной .

3.12. Потенциальная энергия упруго деформированного тела.

Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело (например, сжатая пружина, растянутый стержень и т.п.). В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (например, от расстояния между соседними витками пружины).

Определим работу, которую необходимо затратить для растяжения (или сжатия) пружины на величину «x» (рис.3.8). Будем считать, что пружина подчиняется закону Гука, т.е. упругая сила пропорциональна деформации. Будем проводить растяжение пружины очень медленно, чтобы силу
, с которой мы действуем на пружину, можно было все время считать равной по величине упругой силе
. Далее будем считать, что сила действует в направлении перемещения, т.е.
.

Рис. 3.9

сходя из предыдущего, можно записатьF внешн. =F упр. =kx, гдеx– удлинение пружины,k– коэффициент жесткости пружины, а согласно закону Гука направление упругой силы и перемещения противоположны (силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) и имеют, в конечном счете, электрическую природу).

Пусть под действием силы
пружина растянулась наdx , тогдаdA = F · dx = k · x · dx .

;

Эта работа идет на увеличение потенциальной энергии пружины. В предположении, что потенциальная энергия недеформированной пружины равна «0» (U 1 = 0) получаем

(3.12)

– потенциальная энергия упругой деформации пружины.

3.13. Закон сохранения энергии.

Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m 1 иm 2 . Пусть частицы взаимодействуют друг с другом с силами
и
, модули которых зависят от расстоянияR 12 между частицами. Установлено, что такие силы являютсяконсервативными , т.е. работа, совершаемая такими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть также, кроме внутренних сил на первую частицу действует внешняя консервативная силаи внешняя неконсервативная сила. Аналогично для второй частицы. Тогда уравнения движения частиц можно записать в виде:

Умножим каждое уравнение на
и сложим полученные выражения.

1. Распишем первый член в правой части.

Работа внутренних сил равна . Для замкнутой системы
, а
, гдеи– радиус-векторы частиц.

Учитывая, что силы
и
имеют величину, зависящую только от расстояния и направлены вдоль соединяющей их прямой (это справедливо, например, для сил кулоновского или гравитационного взаимодействий), любую из этих сил можно представить в виде, например,
, гдеf (R 12 ) – некоторая функцияR 12 ,– орт вектора
.

Следовательно,
.

Скалярное произведение
равно приращениюdR 12 расстояния между частицами, тогда
.

Выражение
есть приращение некоторой функции
. Следовательно,

Функция
представляет потенциальную энергию взаимодействия.

Работа внутренних сил будет равна

т.е. не зависит от пути, по которому перемещаются частицы, а определяется начальной и конечной конфигурациями системы. Т.е. силы взаимодействия вида
являются консервативными.

Итак, работа внутренних сил равна убыли потенциальной энергии взаимодействия

2. Второй член представляет работу внешних сил и равен убыли потенциальной энергии системы во внешнем поле консервативных сил

3. Последний член представляет работу неконсервативных внешних сил
.

После этих замечаний можно записать

Величина

T + U вз. + U вн. = E (3.13)

– называется полной механической энергией системы. Если внешние неконсервативные силы отсутствуют, т.е.
, то

Е=const– закон сохранения механической энергии.

ОПРЕДЕЛЕНИЕ: полная механическая энергия системы тел, на которые действуют лишь консервативные силы, остается постоянной.

Для замкнутой системы, т.е. системы, на тела которой не действуют никакие внешние силы, закон сохранения примет вид:

E = T + U вз. = const

Если в замкнутой системе, кроме консервативных сил действуют неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется. Рассматривая консервативные силы как внешние, получим

или после интегрирования
.

Анализ закона сохранения показывает, что полная энергия, оставаясь в консервативной системе величиной постоянной, может переходить из одних видов в другие.

При действии неконсервативных сил возможен переход механической энергии в другие немеханические виды энергии. В этом случае справедлив более общий закон сохранения:

ОПРЕДЕЛЕНИЕ: в изолированной от любых внешних воздействий системе остается постоянной сумма всех видов энергии (включая и немеханические).

К этому добавим, что в природе и технике постоянно имеют место превращения энергии из одних видов в другие. Проиллюстрируем это таблицей.

Процесс или прибор	Превращение энергии
Процесс или прибор
Электрогенератор	механическая	электрическая
Гальванический элемент	химическая	электрическая
Электродвигатель	электрическая	механическая
Зарядка аккумулятора	электрическая	химическая
Фотосинтез	электромагнитная	химическая
Фотоэффект	электромагнитная	электрическая
Ядерный реактор		механическая электромагнитная и др.

Рис. 3.10

таблице не отражено, что при любом превращении часть энергии превращается в теплоту.

Для графического изображения закона сохранения энергии рассмотрим случай, когда тело бросаем вверх.

Если не учитывать силу сопротивления воздуха F сопр. , то систему «тело-Земля» можно рассматривать, как изолированную и консервативную, для которой

E = E к. + U p. = const

Из графика (рис. 3.10) видно, что по мере поднятия тела над поверхностью Земли его потенциальная энергия возрастает от величины U p (h 1) доU p (h 2), но одновременно с этим точно на такую же величину уменьшается кинетическая энергия системыE к. , а полная энергия тела остается величиной постоянной, что соответствует линииBA||h.

Очевидно:

1. При h=0 имеемU p =0, аE=E к. , что соответствует линии ОВ;

2. При h = max имеем U p = max (E к. = 0), аE=U p , что соответствует линииAC.

САМОСТОЯТЕЛЬНО:

Упругий и неупругий центральный удар шаров;

Условия равновесия механической системы.

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами т и М ,находящихся на расстоянии r одна от другой, равна

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е p = 0) принят при r = ∞. Потенциальная энергия гравитационного взаимодействия тела массой т с Землей,где h – высота тела над поверхностью Земли, М 3 – масса Земли, R 3 – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

(12)

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой т с Землей для малых высот h (h « R 3)равна

Е p = m∙g∙h ,

где – модуль ускорения свободного падения вблизи поверхности Земли.

Потенциальная энергия упруго деформированного тела

Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x 1 до конечного значения x 2 (рис. 4, б, в).

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т. к. сила упругости линейно зависит от x ) и умножить на модуль перемещения:

(13)

где Отсюда

(14)

Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:

Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:

А = –(Е р 2 – Е р 1). (16)

Если x 2 = 0 и x 1 = х , то, как видно из формул (14) и (15),

Е р = А.

Тогда физический смысл потенциальной энергии деформированного тела

потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Механическая работа - физическая величина, равная произведению модуля силы на модуль перемещения и косинус угла между нимиA=Fscosα (см. рис.). Работа - величина скалярная (число, не вектор). Измеряется работа в джоулях (Дж). 1 Дж - это работа, совершаемая силой в 1 Н на перемещение 1 м. В зависимости от направлений векторов силы (F) и перемещения (S) механическая работа может быть положительной, отрицательной или равной нулю. Например, если векторы и перпендикулярны, то cos900 = 0 и A = 0. Мощность машины или механизма - это отношение совершенной работы ко времени, в течение которого она совершена . Измеряется мощность в ваттах (Вт), 1 Вт = 1 Дж/с. Простые механизмы: наклонная плоскость, рычаг, блок. Их действие подчиняется«золотому правилу механики»: во сколько раз выигрываем в силе, во столько же раз проигрываем в перемещении. (На практике совершаемая с помощью механизма полная работа всегда несколько больше полезной. Часть работы совершается против силы трения в механизме и перемещения его отдельных частей. Например, применяя подвижный блок, приходится дополнительно совершать работу по поднятию самого блока, веревки и по преодолению силы трения в оси блока. Поэтому для любого механизма полезная работа (AП) всегда меньше, чем полная, затраченная (AЗ). По этой причине КПД = AП/AЗ 100% любого механизма не может быть больше или хотя бы равен 100%).

Мощность - Мощностью N называют величину, равную отношению работы А к промежутку времени t, в течение которого эта работа была совершена:

Из формулы (3.11) следует, что в СИ единицей мощности яв-ляется 1 Дж/с (джоуль в секунду). Эту единицу иначе называют ватт (Вт), 1 Вт= 1 Дж/с.

Связь между мощностью и скоростью при равномерном движении найдем, подставив (3.10) в (3.11):

(Эта формула справедлива и для переменного движения, если под N понимать мгновенную мощность, а под V - мгновенную скорость). Если направление силы совпадает с направлением перемещения, то cosa=1 и N=Fv. Из последней формулы следует, что

Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот. На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств.

Консервативными называются силы, работа которых не зависит от формы траектории, а определяется только положением её начальной и конечной точек. К классу консервативных относятся, например, гравитационные силы, упругие, силы электростатического взаимодействия. Вычислим, например, работу, которую совершает сила тяжести при переходах частицы разными путями из положения 1 в положение 2 (рис. 6.2). Если этот переход произошёл по вертикали, то работа силы :

. (6.11) Теперь пусть та же частица переместится из 1 в 2 по пути 1-1’-2. Здесь промежуточная точка 1’ находится на высоте h2. Рис. 6.2 Полная работа будет складываться из работ силы тяжести на участках 1-1’ и 1’-2: . Работа силы тяжести на горизонтальном участке 1’-2 равна нулю, так как здесь вектор силы нормален перемещению. Мы вновь получили прежний результат, свидетельствующий о том, что работа силы тяжести не зависит от формы траектории. Этот вывод легко обобщается и на случай произвольной криволинейной траектории, соединяющей начальную и конечную точки пути. Гравитационная сила, сила упругости, кулоновская сила электростатического взаимодействия относятся к так называемым центральным силам. Центральными называются силы, направленные к одной и той же точке (либо от неё). Эта точка называется силовым центром. Величина центральной силы зависит только от расстояния до силового центра r (рис. 6.3). Рис. 6.3 Покажем, что все центральные силы консервативны. Вычислим работу центральной силы на участке 1-2 произвольной траектории (рис. 6.3). Элементарная работа силы на участке : . Здесь dSr = dSCosα - проекция вектора перемещения на направление силы (или r). Эта проекция представляет собой изменение расстояния dr до силового центра. Значит: dA = F(r)dr. Работа на конечном пути:

. Так как по определению величина центральной силы есть функция только расстояния r, то значение определённого интеграла будет зависеть только от величин r1 и r2, и не будет зависеть от формы траектории. Можно дать иное определение консервативной силы. Рассмотрим перемещение частицы из положения 1 в положение 3 под действием консервативной силы

(рис. 6.4). Рис. 6.4 Работа, совершаемая при этом силой , не зависит формы от траектории, то есть

. Теперь вычислим работу этой же силы на замкнутом пути 1-2-3-4-1. понятно, что её можно представить суммой работ на участках 1-2-3 и 3-4-1

При этом . Отсюда можно заключить, что работа консервативной силы по любому замкнутому пути равна нулю . Силы, работа которых на замкнутом пути не равна нулю, называются неконсервативными. К числу таких сил относятся, например, сила трения и сила вязкого сопротивления. Легко понять, что при движении частицы по замкнутому контуру работа подобных сил будет отрицательной.

«Физика - 10 класс»

В чём выражается гравитационное взаимодействие тел?
Как доказать наличие взаимодействия Земли и, например, учебника физики?

Как известно, сила тяжести - консервативная сила. Теперь найдём выражение для работы силы тяготения и докажем, что работа этой силы не зависит от формы траектории, т. е. что сила тяготения также консервативная сила.

Напомним, что работа консервативной силы по замкнутому контуру равна нулю.

Пусть тело массой m находится в поле тяготения Земли. Очевидно, что размеры этого тела малы по сравнению с размерами Земли, поэтому его можно считать материальной точкой. На тело действует сила тяготения

где G - гравитационная постоянная,
М - масса Земли,
r - расстояние, на котором находится тело от центра Земли.

Пусть тело перемещается из положения А в положение В по разным траекториям: 1) по прямой АВ; 2) по кривой АА"В"В; 3) по кривой АСВ (рис. 5.15)

1. Рассмотрим первый случай. Сила тяготения, действующая на тело, непрерывно уменьшается, поэтому рассмотрим работу этой силы на малом перемещении Δr i = r i + 1 - r i . Среднее значение силы тяготения равно:

где r 2 сpi = r i r i + 1 .

Чем меньше Δri, тем более справедливо написанное выражение r 2 сpi = r i r i + 1 .

Тогда работу силы F сpi , на малом перемещении Δr i , можно записать в виде

Суммарная работа силы тяготения при перемещении тела из точки А в точку В равна:

2. При движении тела по траектории АА"В"В (см. рис. 5.15) очевидно, что работа силы тяготения на участках АА" и В"В равна нулю, так как сила тяготения направлена к точке О и перпендикулярна любому малому перемещению по дуге окружности. Следовательно, работа будет также определяться выражением (5.31).

3. Определим работу силы тяготения при движении тела от точки А к точке В по траектории АСВ (см. рис. 5.15). Работа силы тяготения на малом перемещении Δs i равна ΔА i = F срi Δs i cosα i ,..

Из рисунка видно, что Δs i cosα i = - Δr i , и суммарная работа опять же будет определяться по формуле (5.31).

Итак, можно сделать вывод, что А 1 = А 2 = А 3 , т. е. что работа силы тяготения не зависит от формы траектории. Очевидно, что работа силы тяготения при перемещении тела по замкнутой траектории АА"В"ВА равна нулю.

Сила тяготения - консервативная сила.

Изменение потенциальной энергии равно работе силы тяготения, взятой с обратным знаком:

Если выбрать нулевой уровень потенциальной энергии на бесконечности, т. е. Е пВ = 0 при r В → ∞, то следовательно,

Потенциальная энергия тела массой m, находящегося на расстоянии r от центра Земли, равна:

Закон сохранения энергии для тела массой m, движущегося в поле тяготения, имеет вид

где υ 1 - скорость тела на расстоянии r 1 от центра Земли, υ 2 - скорость тела на расстоянии r 2 от центра Земли.

Определим какую минимальную скорость надо сообщить телу вблизи поверхности Земли, чтобы оно в отсутствие сопротивления воздуха могло удалиться от неё за пределы сил земного притяжения.

Минимальную скорость, при которой тело в отсутствие сопротивления воздуха может удалиться за пределы сил земного притяжения, называют второй космической скоростью для Земли .

На тело со стороны Земли действует сила тяготения, которая зависит от расстояния центра масс этого тела до центра масс Земли. Поскольку неконсервативных сил нет, полная механическая энергия тела сохраняется. Внутренняя потенциальная энергия тела остаётся постоянной, так как оно не деформируется. Согласно закону сохранения механической энергии

На поверхности Земли тело обладает и кинетической, и потенциальной энергией:

где υ II - вторая космическая скорость, М 3 и Я 3 - соответственно масса и радиус Земли.

В бесконечно удаленной точке, т. е. при r → ∞, потенциальная энергия тела равна нулю (W п = 0), а так как нас интересует минимальная скорость, то и кинетическая энергия также должна быть равна нулю: W к = 0.

Из закона сохранения энергии следует:

Эту скорость можно выразить через ускорение свободного падения вблизи поверхности Земли (при расчётах, как правило, этим выражением пользоваться удобнее). Поскольку то GM 3 = gR 2 3 .

Следовательно, искомая скорость

Точно такую же скорость приобрело бы тело, упавшее на Землю с бесконечно большой высоты, если бы не было сопротивления воздуха. Заметим, что вторая космическая скорость в раза больше, чем первая.

Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например: механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и др.

Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.

Механическая энергия Е характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.

Кинетическая энергия

Рассмотрим случай, когда на тело массой m действует постоянная сила \(~\vec F\) (она может быть равнодействующей нескольких сил) и векторы силы \(~\vec F\) и перемещения \(~\vec s\) направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F ∙s . Модуль силы по второму закону Ньютона равен F = m∙a , а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ 1 и конечной υ 2 скорости и ускорения а выражением \(~s = \frac{\upsilon^2_2 - \upsilon^2_1}{2a}\) .

Отсюда для работы получаем

\(~A = F \cdot s = m \cdot a \cdot \frac{\upsilon^2_2 - \upsilon^2_1}{2a} = \frac{m \cdot \upsilon^2_2}{2} - \frac{m \cdot \upsilon^2_1}{2}\) . (1)

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела .

Кинетическая энергия обозначается буквой E k .

\(~E_k = \frac{m \cdot \upsilon^2}{2}\) . (2)

Тогда равенство (1) можно записать в таком виде:

\(~A = E_{k2} - E_{k1}\) . (3)

Теорема о кинетической энергии

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения υ , то работа силы равна конечному значению кинетической энергии тела:

\(~A = E_{k2} - E_{k1}= \frac{m \cdot \upsilon^2}{2} - 0 = \frac{m \cdot \upsilon^2}{2}\) . (4)

Физический смысл кинетической энергии

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

Потенциальная энергия

Потенциальная энергия – это энергия взаимодействия тел.

Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Потенциальными называются силы , работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.

При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.

Силы , работа которых зависит от формы траектории, называются непотенциальными . При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.

Потенциальная энергия взаимодействия тела с Землей

Найдем работу, совершаемую силой тяжести F т при перемещении тела массой m вертикально вниз с высоты h 1 над поверхностью Земли до высоты h 2 (рис. 1). Если разность h 1 – h 2 пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F т во время движения тела можно считать постоянной и равной mg .

Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна

\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)

Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F т = m∙g совершает работу

\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)

где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.

Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h ’, h ’’ и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:

\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\) , (7)

где h 1 и h 2 – высоты от поверхности Земли, на которых расположены соответственно точки В и С .

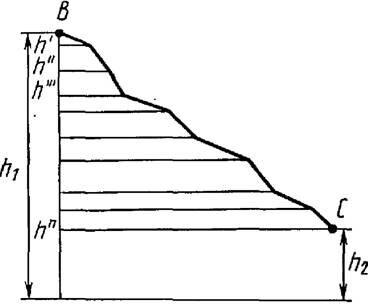
Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.

При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.

Равенство (7) можно представить в таком виде:

\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)

Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h 2 , в точку, расположенную на высоте h 1 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.

\(~A = - (E_{p2} - E_{p1})\) . (9)

Потенциальная энергия обозначается буквой Е p .

Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

При таком выборе нулевого уровня потенциальная энергия Е p тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:

\(~E_p = m \cdot g \cdot h\) . (10)

Физический смысл потенциальной энергии взаимодействия тела с Землей

потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.

В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m , находящееся на высоте h , где h < h 0 (h 0 – нулевая высота), обладает отрицательной потенциальной энергией:

\(~E_p = -m \cdot g \cdot h\) .

Потенциальная энергия гравитационного взаимодействия

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и М , находящихся на расстоянии r одна от другой, равна

\(~E_p = G \cdot \frac{M \cdot m}{r}\) . (11)

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е p = 0) принят при r = ∞.

Потенциальная энергия гравитационного взаимодействия тела массой m с Землей, где h – высота тела над поверхностью Земли, M e – масса Земли, R e – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

\(~E_e = G \cdot \frac{M_e \cdot m \cdot h}{R_e \cdot (R_e +h)}\) . (12)

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой m с Землей для малых высот h (h « R e) равна

\(~E_p = m \cdot g \cdot h\) ,

где \(~g = G \cdot \frac{M_e}{R^2_e}\) – модуль ускорения свободного падения вблизи поверхности Земли.

Потенциальная энергия упруго деформированного тела

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т.к. сила упругости линейно зависит от x ) и умножить на модуль перемещения:

\(~A = F_{upr-cp} \cdot (x_1 - x_2)\) , (13)

где \(~F_{upr-cp} = k \cdot \frac{x_1 - x_2}{2}\) . Отсюда

\(~A = k \cdot \frac{x_1 - x_2}{2} \cdot (x_1 - x_2) = k \cdot \frac{x^2_1 - x^2_2}{2}\) или \(~A = -\left(\frac{k \cdot x^2_2}{2} - \frac{k \cdot x^2_1}{2} \right)\) . (14)

\(~E_p = \frac{k \cdot x^2}{2}\) . (15)

\(~A = -(E_{p2} - E_{p1})\) . (16)

Если x 2 = 0 и x 1 = х , то, как видно из формул (14) и (15),

\(~E_p = A\) .

Физический смысл потенциальной энергии деформированного тела

Потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия – движущиеся тела. И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Рассмотрим вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему.

Замкнутая система – это система, на которую не действуют внешние силы или действие этих сил скомпенсировано . Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:

\(~A = -(E_{p2} - E_{p1})\) . (17)

По теореме о кинетической энергии, работа тех же сил равна изменению кинетической энергии:

\(~A = E_{k2} - E_{k1}\) . (18)

Из сравнения равенств (17) и (18) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:

\(~E_{k2} - E_{k1} = -(E_{p2} - E_{p1})\) или \(~E_{k1} + E_{p1} = E_{k2} + E_{p2}\) . (19)

Закон сохранения энергии в механических процессах :

сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и си-лами упругости, остается постоянной.

Сумма кинетической и потенциальной энергии тел называется полной механической энергией .

Приведем простейший опыт. Подбросим вверх стальной шарик. Сообщив начальную скорость υ нач, мы придадим ему кинетическую энергию, из-за чего он начнет подниматься вверх. Действие силы тяжести приводит к уменьшению скорости шарика, а значит, и его кинетической энергии. Но шарик поднимается выше и выше и приобретает все больше и больше потенциальной энергии (Е p = m∙g∙h ). Таким образом, кинетическая энергия не исчезает бесследно, а происходит ее превращение в потенциальную энергию.

В момент достижения верхней точки траектории (υ = 0) шарик полностью лишается кинетической энергии (Е k = 0), но при этом его потенциальная энергия становится максимальной. Дальше шарик меняет направление движения и с увеличивающейся скоростью движется вниз. Теперь происходит обратное превращение потенциальной энергии в кинетическую.

Закон сохранения энергии раскрывает физический смысл понятия работы :

работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, – уменьшению потенциальной энергии тел. Следовательно, работа равна энергии, превратившейся из одного вида в другой.

Закон об изменении механической энергии

Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил:

\(~A_{vn} = \Delta E = E - E_0\) . (20)

где Е и Е 0 – полные механические энергии системы в конечном и начальном состояниях соответственно.

Примером такой системы может служить система, в которой наряду с потенциальными силами действуют непотенциальные силы. К непотенциальным силам относятся силы трения. В большинстве случаев, когда угол между силой трения F r тела составляет π радиан, работа силы трения отрицательна и равна

\(~A_{tr} = -F_{tr} \cdot s_{12}\) ,

где s 12 – путь тела между точками 1 и 2.

Силы трения при движении системы уменьшают ее кинетическую энергию. В результате этого механическая энергия замкнутой неконсервативной системы всегда уменьшается, переходя в энергию немеханических форм движения.

Например, автомобиль, двигавшийся по горизонтальному участку дороги, после выключения двигателя проходит некоторый путь и под действием сил трения останавливается. Кинетическая энергия поступательного движения автомобиля стала равной нулю, а потенциальная энергия не увеличилась. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. Следовательно, в результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.

Закон сохранения и превращения энергии

при любых физических взаимодействиях энергия превращается из одной формы в другую.

Иногда угол между силой трения F tr и элементарным перемещением Δr равен нулю и работа силы трения положительна:

\(~A_{tr} = F_{tr} \cdot s_{12}\) ,

Пример 1 . Пусть, внешняя сила F действует на брусок В , который может скользить по тележке D (рис. 5). Если тележка перемещается вправо, то работа силы трения скольжения F tr2 , действующей на тележку со стороны бруска, положительна:

Пример 2 . При качении колеса его сила трения качения направлена вдоль движения, так как точка соприкосновения колеса с горизонтальной поверхностью двигается в направлении, противоположном направлению движения колеса, и работа силы трения положительна (рис. 6):

Литература

Кабардин О.Ф. Физика: Справ. материалы: Учеб. пособие для учащихся. – М.: Просвещение, 1991. – 367 с.
Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
Элементарный учебник физики: Учеб. пособие. В 3 т. / Под ред. Г.С. Ландсберга: т. 1. Механика. Теплота. Молекулярная физика. – М.: Физматлит, 2004. – 608 с.
Яворский Б.М., Селезнев Ю.А. Справочное руководство по физике для поступающих в вузы и самообразования. – М.: Наука, 1983. – 383 с.